Yesterday I tackled a vexing problem: Is general relativity really that hard to understand? In one sense, of course it is. But when it receives the treatment that most scientific theories are given, I’d say no. For example, here’s how Newton’s theory of gravitation is usually described for laymen:
- All objects with mass (for example, the earth and the moon) are attracted to each other. The bigger the mass, the stronger the attraction.
- The attraction decreases as the objects get farther apart. If they’re twice as far apart, the attraction is one-fourth. If they’re three times as
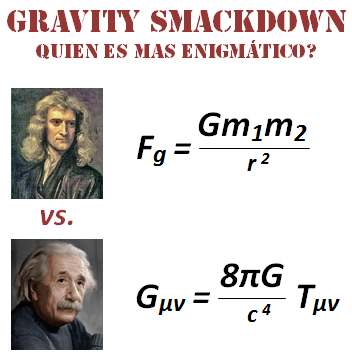far apart, the attraction is one-ninth. Etc.
Easy peasy! Objects are attracted to each other via certain mathematical rules. But hold on. This is only easy because we’ve left out all the hard stuff. Why are massive objects attracted to each other? Newton himself didn’t even try to guess, famously declaring “I frame no hypotheses.” Action-at-a-distance remained a deep and profound mystery for centuries.1 And another thing: why does the gravitational attraction decrease by exactly the square of the distance? That’s suspiciously neat. Why not by the power of 2.1 or the cube root of e? And nothing matters except mass and distance? Why is that? This kind of stuff is almost never mentioned in popular descriptions, and it’s the reason Newton’s theory is so easy to picture: It’s because we don’t usually give you anything to picture in the first place. Apples fall to the earth and planets orbit the sun. End of story.
Well then, let’s describe Einstein’s theory of gravity—general relativity—the same way:
- Objects with mass are attracted to each other.
- The attraction decreases as the objects get farther apart. Einstein’s equation is different from Newton’s, so the amount of the decrease is slightly different too.
- In Einstein’s theory, gravity isn’t a property of mass. It’s caused by the geometry of the universe, so it affects everything, including energy.
- Light is a form of energy, so beams of light are slightly bent when they travel near massive objects like stars.
- Einstein’s equations predict that time runs slower near objects with high gravitational fields.
- Sometimes an object can have such a strong gravitational field that light can’t escape and time stops. These are called black holes.
- Plus a few other intriguing but fairly minor deviations from Newton’s theory.
Not so hard! Once again, there’s nothing to picture even though this is a perfectly adequate lay description of general relativity. The trouble starts when we do what we didn’t do for Newton: ask why all this stuff happens. But guess what? In any field of study, things get more complicated and harder to analogize as you dive more deeply. For some reason, though, we insist 
on doing this for relativity even though we happily ignore it in descriptions of Newton’s theory of gravity. And this is when we start getting accelerating elevators in space and curved spacetime and light cones and time dilation. Then we complain that we don’t understand it.
(By the way: if you study classical Newtonian gravity, it turns out to be really complicated too! Gravitation, the famous Misner/Thorne/Wheeler doorstop on general relativity, is 1200 difficult pages. But guess what? Moulton’s Introduction to Celestial Mechanics pushes 500 pages—and it only covers a fraction of classical gravitation. This stuff is hard!)
Relativity and quantum mechanics are both famously hard to grasp once you go beyond what they say and demand to know what they mean. In truth, they don’t “mean” anything. They do gangbusters at describing what happens when certain actions are taken, and we can thank them for transistors, GPS satellites, atom bombs, PET scans, hard drives, solar cells, and plenty of other things. The mathematics is difficult, but often it looks kinda sorta like the math for easier concepts. So quantum mechanics has waves and probability amplitudes because some of the math looks pretty similar to the math we use to describe ocean swells and flipping coins. Likewise, general relativity has curved spacetime because Einstein’s math looks a lot like the math we use to describe ordinary curved objects.
But is it really probability? Is it really a four-dimensional curve? Those are good ways to interpret the math. But you know what? No matter how much you dive in, you’ll never know for sure if these interpretations of the math into human-readable form are really correct. You can be confident the math is correct,2 but the interpretations will always be a bit iffy. And sadly, they won’t really help you understand the actual operation of these theories anyway. Objects with mass attract each other, and if you know the math you can figure out exactly how much they attract each other. Calling the path of the objects a geodesic on a 4-dimensional curved spacetime manifold doesn’t really make things any clearer. In all likelihood, a picture of a bowling ball on a trampoline doesn’t either.
But we keep trying. We just can’t help thinking that everything has to be understandable to the h. sapiens brain. This makes interpreting difficult math an excellent way to pass the time for a certain kind of person. It’s a lot like trying to interpret the actions of the Kardashian family. Lots of fun, but ultimately sort of futile if you’re just an ordinary schmoe.
1General relativity and quantum mechanics finally put everyone’s minds at ease by showing that the action wasn’t actually at a distance after all. Unfortunately, they explained one mystery only at the cost of hatching a whole bunch of others.
2We hope so, anyway. But then, Newton’s math looked pretty damn good for a couple of centuries before it turned out to be slightly wrong. That may yet happen to general relativity and quantum mechanics too.
UPDATE: I’ve modified the third bullet of the relativity list to make it more accurate.
