Over at the Washington Monthly, Jill Barshay reports on the latest study comparing math instruction between nations:
Researchers looked at math instruction in 64 countries and regions around the world, and found that the difference between the math scores of 15-year-old students who were the most exposed to pure math tasks and those who were least exposed was the equivalent of almost two years of education. The research was based on how students answered survey questions that accompanied an international test, called the Programme for International Student Assessment, or PISA.
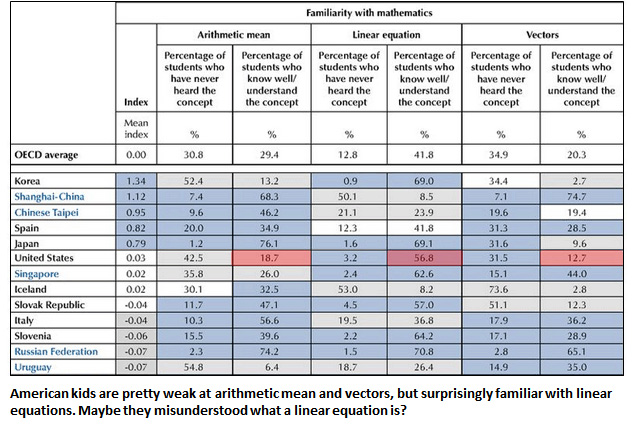
The result was surprising for two reasons. First, the PISA exam itself is largely a test of applied math, not equation-solving….It’s also surprising because many veteran educators recommend using real-world applications of abstract math concepts as a motivational tool. And the OECD doesn’t disagree. But real-world examples aren’t enough. Students still need to learn the broad concepts and the mathematical notation. In South Korea, for example, students get a big dose of both applied and pure math instruction and they score among the top 10 in the world.
I browsed through the report myself, and unless I missed something I can’t say that these results surprise me even slightly. As the report notes, kids are tracked into different kinds of math instruction in most schools, and the brighter kids are therefore exposed to more advanced math than the others. That’s both normal and necessary, and the only real question is whether it’s done properly. If poor kids are tracked into less advanced classes at unfairly high levels, then we have a problem. Here’s what the report says about that:
Across the OECD countries, socio-economic differences among students and schools account for around 9% — and some countries, as much as 20% — of the variation in familiarity with mathematics concepts.
That’s surprising all right, but mainly because 9 percent is a pretty low number. I would have guessed higher. What we’re primarily left with here is that some kids are better at math than others; those who are good at math take more advanced classes; and more advanced classes expose them to more abstract concepts. So where’s the surprise?
As for the ability to solve real-world problems, there’s no surprise there either. I doubt the difference is due to the kinds of math the kids are exposed to. It’s due to the fact that some kids are better at math than others in the first place and have taken more advanced classes. The PISA exam may be a test of applied math, but obviously you have to know the underlying pure math too.
Finally, one related note: I’ve always wondered about the use of using real-world problems as a “motivational tool.” The problem is that once you get past the level of basic arithmetic, real-world problems tend to be pretty artificial. There just aren’t very many real-world applications of high school algebra or geometry, and I’ve often wondered if story problems only make that more obvious. In introductory algebra, for example, you often get problems about trains meeting or how much of a head start someone on foot needs to get somewhere before a car would. Those are so obviously non-useful, though, that they also seem non-motivational. If this is all you can do with algebra, why bother?
I don’t think there’s a good answer to this. Real life just doesn’t require much in the way of algebra or geometry for most people. But I guess you have to try.