If you’re looking for Kevin, you can find him here starting on February 1:

Kevin Drum
A blog of my opinions. Plus charts and cats.
-

After 12½ years at Mother Jones, this is finally it: my last blog post. This has, literally, been a dream job, getting paid to do something I’d be happy to do for free. (Which I’m about to prove by continuing to do it for free now that I can afford to.) It’s been a blast the whole time and it’s lasted far longer than I ever had any right to expect.
In addition to everything else, I especially want to thank my two main editors. Monika Bauerlein was my primary editor for the first seven years, always providing light but sneakily incisive suggestions for my magazine pieces. I don’t think I’ve ever mentioned this, but I especially want to thank her for her editing of my piece on lead and crime. It’s the most important piece I ever wrote for MoJo and her edits were instrumental in improving a number of weak spots in my initial draft.
After Monika was named CEO in 2015, Clara Jeffery took over primary editing duties on my magazine pieces. To this day I don’t know for sure how much difference that made, since Clara and Monika seem to be joined at the hip, but Clara pushed me to write several of my best pieces. I think I argued with Clara more than I did with Monika, but her edits and questions always forced me to think about what I really wanted to say and whether there was a better way to say it.
I hope everyone sticks around and continues reading Mother Jones, which is not just a great magazine but also a different kind of magazine that covers more than just the usual turf of political reporting. Of course, I also hope you’ll continue reading me. Starting on Monday morning, you can find me here.
-
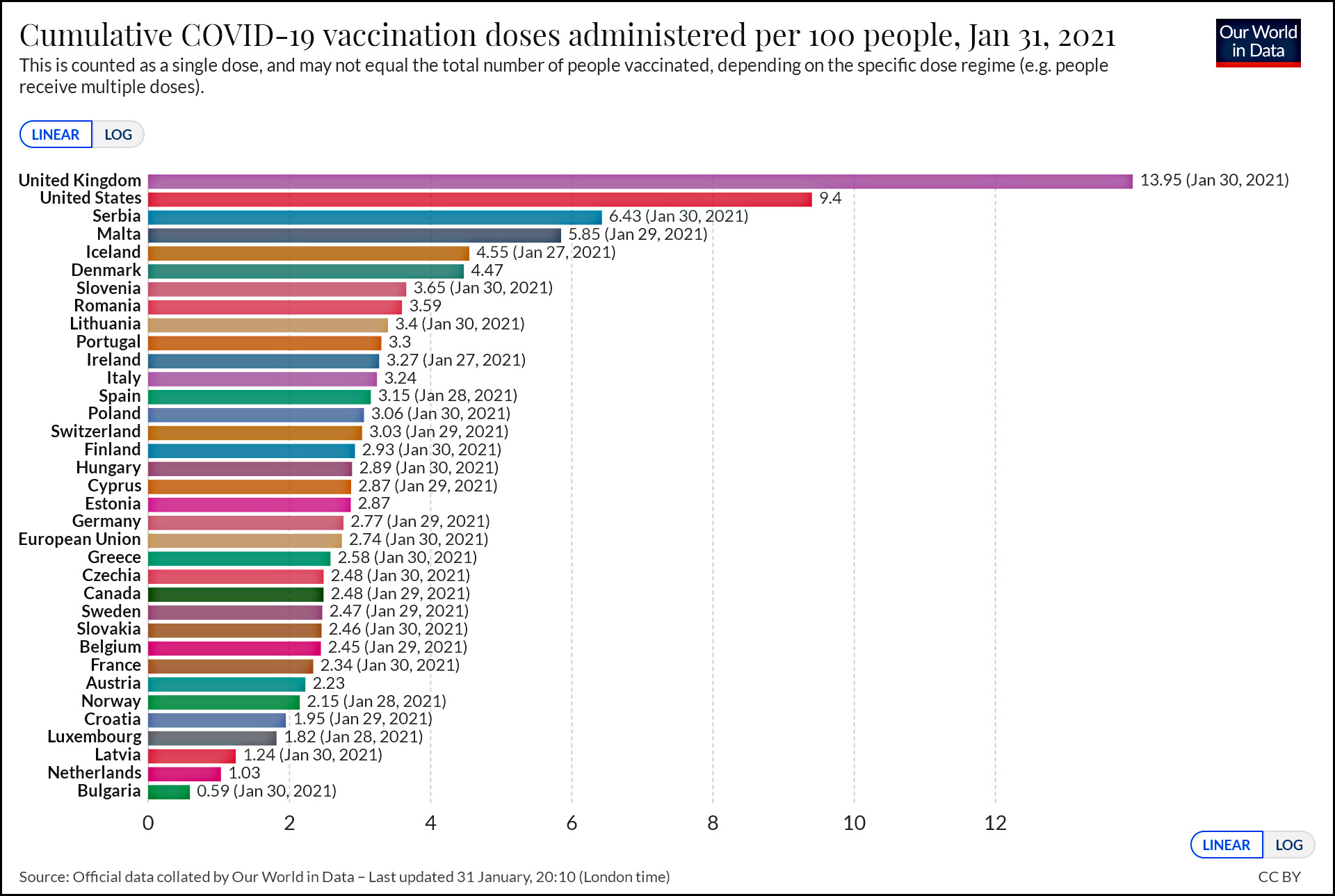
As of the end of the month, here’s where we stand on vaccinations compared to every country in Europe. Note that this counts the number of doses, not the number of people vaccinated, since some people have already received two doses.
Some countries are doing better than others, but overall the US is at 9.4 compared to an EU average of 2.74.
-

Carol Guzy/ZUMA
Former President Trump has parted ways with his lead impeachment lawyers just over a week before his Senate trial is set to begin, two people familiar with the situation said Saturday. Butch Bowers and Deborah Barbier, both South Carolina lawyers, are no longer with Trump’s defense team….Greg Harris and Johnny Gasser, two former federal prosecutors from South Carolina, are also off the team, one of the people said.
According to a different person with knowledge of the legal hires, Bowers and Barbier left the team because Trump wanted them to use a defense that relied on allegations of election fraud, and the lawyers were not willing to do so….Trump has struggled to find attorneys willing to defend him after becoming the first president in history to be impeached twice….After numerous attorneys who defended him previously declined to take on the case, Trump was introduced to Bowers by one of his closest allies in the Senate, South Carolina Sen. Lindsey Graham.
Jokes aside, this shows that Trump understands what Bowers didn’t: this isn’t a trial, it’s a TV show. Trump knows that his control over the Republican Party is still strong enough that he faces no chance of conviction, which means that legal arguments are unnecessary. Instead, he wants this to be a nationally televised opportunity for him to persuade the public that the 2020 election was teeming with Democratic fraud that cheated him out of reelection. He will, of course, be aided in this via coverage from Fox News, Rush Limbaugh, and all the rest of the right-wing media empire. I predict high ratings.
-
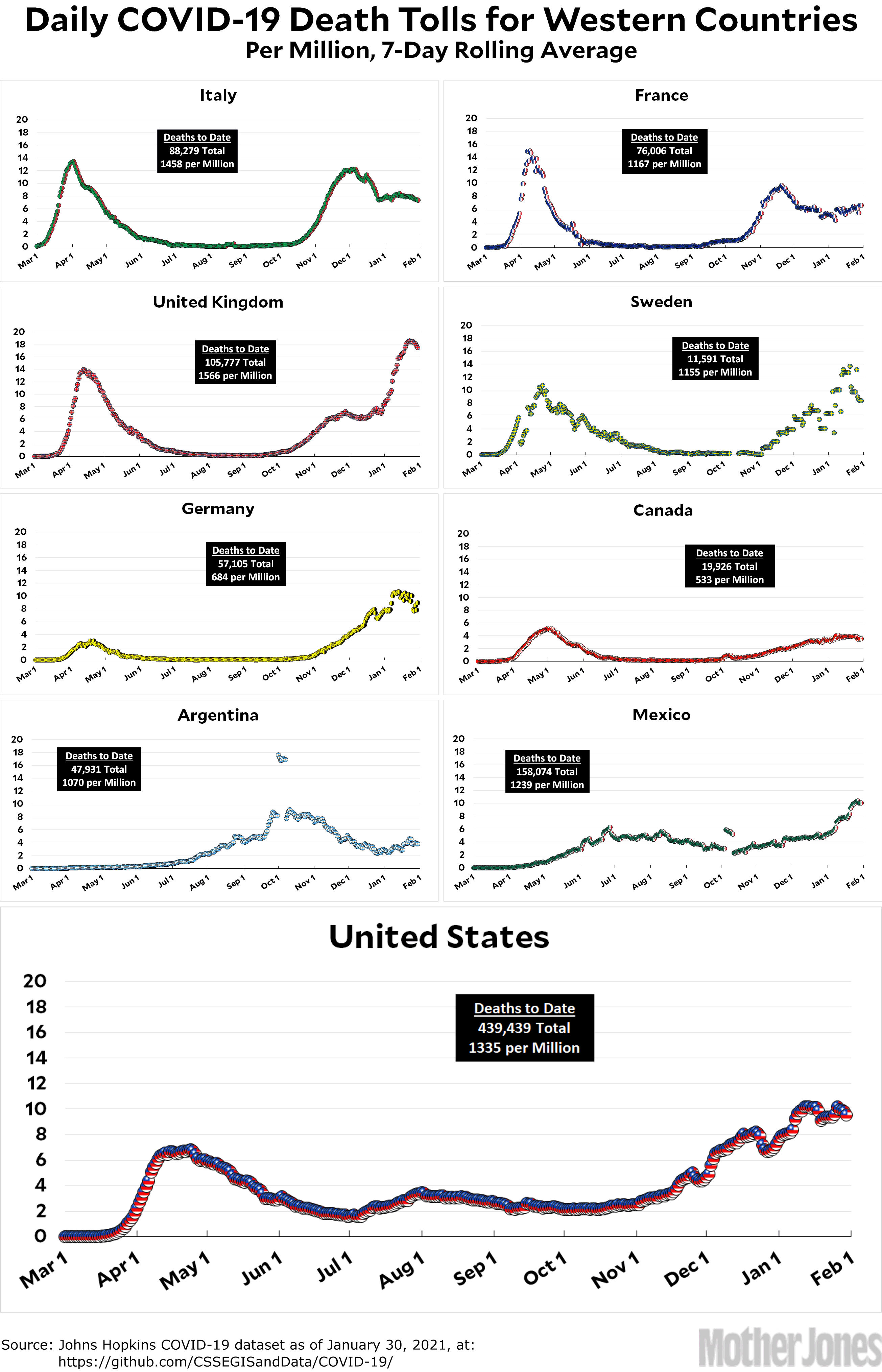
Here’s the officially reported coronavirus death toll through January 30. The raw data from Johns Hopkins is here.
-
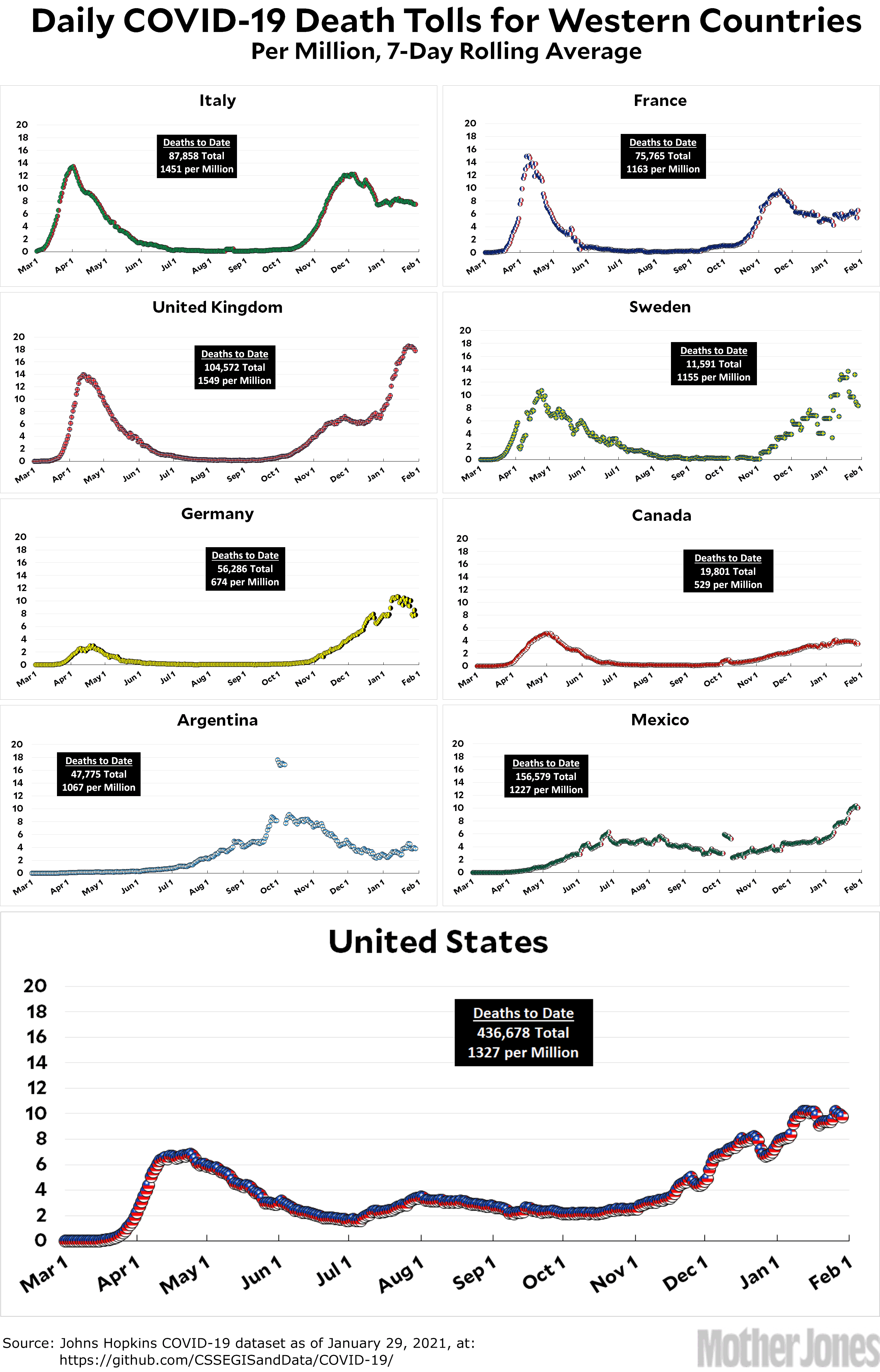
Here’s the officially reported coronavirus death toll through January 29. The raw data from Johns Hopkins is here.
-
In her quest to drink water from every possible receptacle, Hopper found something new this morning. Our neighbor’s trash can fell over in the night and the lid filled up with lovely, tasty rainwater. What more could a cat want?

-

Mary Evans via ZUMA
Today is my last full day at Mother Jones, although I’ll be around for the rest of the weekend and blogging as the mood hits me. With that in mind, I want to outline my take on what’s wrong with politics in the US these days. I’ve gone over the details of each of these points before, and I have a half-written long version of this as well. For now, though, I want to present it in the simplest, clearest possible way.
My goal here is not really to convince you I’m right. It’s just to get you thinking. Here it is:
- In material terms, the United States is in pretty good shape. Incomes are up; crime is down; financial satisfaction is high; and overall happiness is stable. This does not mean we have no problems. It merely means that our problems are not any worse than they’ve ever been.
- Democracy is in pretty good shape too. The Trump insurrection was scary, but it was a one-off. Overall, elections are held normally; voter turnout is stable; Black turnout is up; we have greater diversity in Congress; and the attempt to challenge the 2020 election was a dismal failure.
- Much of the distress over politics is due to the fact that the country has been stuck in a 50-50 pattern for so long. This kind of endless trench warfare irritates everyone. But it’s not a sign of instability. It’s just a sign that neither party has done a very good job of building a large and durable majority. It’s also a sign that few people are terrifically unhappy over our current situation.
- Nevertheless, what fundamentally defines modern politics is that we’re all scared. That is, we’re scared of the other party. Why?
- It isn’t because we’re more prone to conspiracy theories these days. The evidence suggests that belief in conspiracy theories has been fairly stable since the 1960s. Nor is it because of social media. This fear goes back to at least the year 2000, far before social media had any impact. And obviously it isn’t because the US is facing ruin. We aren’t.
- The reason is simple: Fox News. Newt Gingrich may have been the original prophet of fear, but it was Fox News that executed his vision and then gained a national following in the early 2000s. Fox broadcasts are dedicated almost exclusively to scaring the hell out of their audience about what Democrats will do if they gain power. They will tax your money away. They will give your money to Black people. They will crush Christianity. They want government bureaucrats to control every aspect of your life. They want schools to teach your kids that gay sex is good and patriotism is bad.
- This is the explanation for the most fundamental question everyone should be asking about the 1/6 insurrection: what on earth scared so many people so badly that they were willing to storm the Capitol in order to keep Joe Biden from becoming president?
There are two things we can do about this culture of fear. First, liberals need to avoid going down the same rabbit hole as conservatives. We’re not close to that yet, but there’s not much question that we’ve been moving in that direction. It needs to stop.
Second, and most important, we need to mount some kind of broad, aggressive battle against Fox News. This obviously needs to be a fully private battle, and it needs to be waged in every possible way. We can boycott advertisers. We can pressure cable companies. We can air commercials that take on the fear machine. We can even compromise on some of the political positions that conservatives find most unnerving.
In general, we need to do everything we can to reduce the fear that conservatives have of liberal rule. You may think this is unfair: why should it be our responsibility to do this? But that’s politics. Our job is to win converts, and fair or not, this is the way to do it.
I don’t think a single blog post is going to convince a lot of people. Fair enough. But spend a little time thinking about this. Roll it around in your head. Compare it to other theories and you’ll find that most of them don’t really hold water. In the end, we need a no-holds-barred battle against Fox News and a massive PR campaign to persuade the conservative rank and file that Democrats don’t, in fact, want to send them off to reeducation camps. This is the only way to get American politics back on track.
-

Ron Sachs/CNP/ZUMA
Eric Cantor was one of the “young guns” of the Republican Party until 2014, when he was suddenly deemed insufficiently conservative and lost to a fellow named Dave Brat in a primary challenge. Today, in the Washington Post, Cantor warns that Republicans are in trouble because they aren’t willing to tell their constituents the truth. But it doesn’t have to be this way:
If the majority of Republican elected officials work together to confront the false narratives in our body politic — that the election was stolen (it wasn’t), that there is a QAnon-style conspiracy to uproot pedophiles at the heart of American government (there isn’t), that a Democratic-controlled government means the end of America (it doesn’t; it may produce worse policy, but the republic has survived 88 years of Democrats occupying the White House) — all Republicans will be better off. If instead most elected Republicans decide to protect themselves against a primary challenge through their silence or even their affirmation, then like the two prisoners acting only in their own interests, we will all be worse off. (The same holds true for Democrats.)
Cantor is right: there is a widespread belief among rank-and-file Republicans that Democrats are deliberately trying to ruin the country because they hate America. This needs to stop if our political system is to have any chance of thriving.
Of course, Cantor doesn’t mention why so many Republicans believe this. Maybe he still has too many friends who like to appear on Fox News.
-
I’m not super interested in the whole GameStop fiasco, but a paragraph in a New York Times piece caught my attention last night. A lot of the trades that have sent GameStop into the stratosphere were made via Robinhood, a trading app that charges no fees. So how do they make money?
Without fees, Robinhood makes money by passing its customer trades along to bigger brokerage firms, like Citadel, who pay Robinhood for the chance to fulfill its customer stock orders.
Wait. Robinhood can’t make money with $0 fees, but Citadel can apparently make money with essentially negative fees. I’m no high finance guy, but what am I missing here?
UPDATE: A reader answers my question:
There is value in the “flow” itself. Market makers (like Citadel or others) earn return by buying and selling particular stocks. If they have a ton of orders, buys and sells, at different prices, they can fill those orders in such a way as to earn a spread on each transaction (or really the totality of transactions as they are essentially wholesalers). This is how trading works. Commissions are just like a processing fee. That’s not how trading desks make money.
Huh. Somehow this still seems like a good way to lose a ton of money if things go pear shaped. But my money is all in low-load mutual funds, so what do I know?



