
<a href="http://www.shutterstock.com/pic-172082663/stock-photo-handsome-young-school-boy-thinking-about-complex-mathematical-signs.html?src=wAGEU8fxVzuEQly3akGD-A-1-72">ra2studio</a>/Shutterstock
Chances are that when you think about math—which, for most of us, happens pretty infrequently—you don’t think of it in anything like the way that Jordan Ellenberg does. Ellenberg is a rare scholar who is both a math professor (at the University of Wisconsin-Madison) and a novelist. And in his fascinating new book, How Not to Be Wrong: The Power of Mathematical Thinking, he deploys analyses of poetry, politics, and even religion in a bold recasting of what math is in the first place.
For Ellenberg, all the stuff you hated about math in high school isn’t the core of the thing. He’s emphatic that mathematics isn’t simply about the calculations involving, you know, numbers; rather, it’s a highly nuanced approach to solving problems that we all, unavoidably, encounter. Ellenberg’s chapters range from showing how mathematical thinking undermines many popular proofs for the existence of God (Paley’s design argument, Pascal’s wager), to explaining how math helps us understand why smoking causes lung cancer (contrary to claims by one early statistician who actually argued that the causation might be reversed—that lung cancer might cause smoking!).
“The symbolic manipulation, and multiplying numbers together, and doing algebra, and computing the derivative of the function—that is to math as typing is to writing,” says Ellenberg on the latest episode of the Inquiring Minds podcast. “You need to be able to do it; it’s part of math. But exactly what I want to fight is the idea that actually thinking is something that takes place separate from the mathematics. It is the mathematics.”

In this recasting, mathematics isn’t just about solving problems, but about figuring out which techniques we ought to use to solve problems, and how much we can really trust the answers they spit out. That means careful thinking about statistics is a key part of mathematics. (Ellenberg spends considerable time explaining why current tests of statistical significance can be so misleading.) So is recognizing when you’re using a mathematical model to think about a problem that isn’t appropriate to that problem (more on this below).
Ultimately, then, mathematics means glimpsing the entire structure of a problem, so that you can figure out how best to attack it, and so that you’ll know how reliable your ultimate answers will be. “That’s when you know you’re doing mathematics,” Ellenberg says. “When you see the skeleton underneath the flesh.”
For instance, Ellenberg is big on busting tendencies towards what he calls “false linearity” in our thinking—and not afraid to use political examples to make his point. Early in the book, he takes on a Cato Institute scholar who wrote a 2010 blog post about health care entitled, “Why Is Obama Trying to Make America More Like Sweden When Swedes Are Trying to Be Less Like Sweden?” As Ellenberg explains, the whole conceit of this argument, the mental model involved, is linear in nature. He includes this amusing hand-drawn figure in the book (one of many) to illustrate the point:

If the United States and Sweden are both on a straight line, one end of which is prosperity and one end of which is a “Black Pit of Socialism,” then of course the US should move away from socialism and towards higher prosperity—and Sweden should too. “But if you take one second to think about that consciously, that’s obviously not true,” Ellenberg explains.
Suppose instead that the two countries are located on a curve, one where prosperity peaks at some degree of socialism/”Swedishness” that is greater than that of the United States but also less than that of Sweden, but declines when you have too much socialism—or too little of it. More like this:
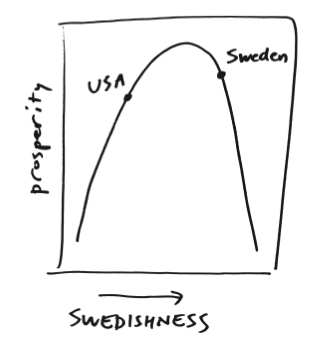
“There’s such a thing as taxing too little, and there’s such a thing as taxing too much, and there’s kind of a Goldilocks point where it’s just right, somewhere in between,” Ellenberg says. “And so there’s no contradiction to say that, maybe the US should have more of a welfare state than it does, and maybe Sweden should have less of a welfare state than it does.”
It’s all about where you are on the curve. For Ellenberg, then, mathematics is the thought process that allows you to recognize when a linear model is wrong, but a more complex curvilinear one is more appropriate to the problem. That involves a lot more than mere calculation. (In the book, Ellenberg also explores the infamous “Laffer curve,” so loved by supply-side economists, which purports shows the relationship between tax rates and government revenue. In this case, Ellenberg doesn’t say that the curve itself is misguided—he just questions some conservative assumptions about where we currently are on that curve, and where we were in the 1980s.)
Although Ellenberg doesn’t make this case explicitly, there’s an argument to be made that the brand of mathematical thinking that he’s embracing overlaps heavily with a broadly liberal style of thinking about politics and the world. Published psychological research has shown, after all, that one important difference between the left and the right involves the toleration of nuance and uncertainty. Liberals tend to be the kind of people who are okay with stewing on things, dwelling on them, not making up their minds, and giving complex and detailed answers; for conservatives, this often comes off as indecisive and wishy-washy.
Ellenberg’s book is nothing if not a celebration of mathematics as a vehicle for nuanced thinking and grappling with uncertainty. On Inquiring Minds, I explained to him why I thought his approach was liberal in a psychological sense. Here’s how he responded:
I think there is a stereotype that mathematicians are exactly the opposite of people who care about nuance. I think most people, if they were to imagine the psychological makeup of a mathematician, they would say, “Oh, that’s somebody who is very black and white, who thinks in ‘yes’ or ‘no,’ very precise ‘down to the tenth decimal place’ terms.” And so I think what you’re pointing to psychologically is very real, and it’s something I try to display in the book. That the mathematical way of thinking, it can be like that, but it’s not the only thing that it is. We valorize uncertainty too, and try to study it and bring it in our orbit.
So is there really anything to the relationship between math and liberalism?
Well, conservatives themselves might say so. After all, they are often busy analyzing the politics of university professors to show their “liberal biases,” and that sometimes includes mathematicians. According to one 2006 study, 72 percent of American university math/science faculty voted for John Kerry, and just 24 percent voted for Bush in 2004. Even more precise is a 2005 study, which found that 69 percent of college mathematics professors identified as liberal. That meant mathematicians were less liberal than denizens of the English department (88 percent) or sociologists (77 percent), but considerably more liberal than economists (55 percent) or business professors (49 percent).

One of the heroes of Ellenberg’s book, the French Revolutionary figure the Marquis de Condorcet, epitomizes the connection between liberalism and mathematical thinking. A leading luminary of the French Enlightenment, Condorcet pioneered what we would today consider social science: The quest to use systematic and numerical analysis to explain social and political behavior (his word for it was “social mathematics”). Condorcet’s theorems for analyzing the votes of juries, and for determining who actually won an election, were his way of trying to use math to get at the truth in politics and in criminal justice—a truth he believed was eminently attainable, if you used the right methods. And only by attaining truth, Condorcet believed, could you actually create a government that worked.
“I would even go so far to say that he’s inventing the kind of idea of political science and social science—the idea that one of the things that we do when we think about what is right and what is just, in politics, is ask numerical questions,” says Ellenberg of Condorcet. “Which is so deeply wound into the way we think about politics now that it’s almost hard to imagine someone inventing it. But it was quite radical.”
In his final chapter, Ellenberg makes his strongest statement about the psychological temperament associated with mathematical thinking. He starts out with a famous speech from Theodore Roosevelt, given in 1910 at the Sorbonne, the home of French academics. On the occasion, Roosevelt praised those who were willing to take action, to take chances in life even if they’re wrong, and derided the “critic” who snipes but doesn’t take decisive action in the metaphorical “arena.” “I pay all homage to intellect and to elaborate and specialized training of the intellect,” Roosevelt told the assemblage of French scholars, “and yet…more important still are the commonplace, everyday qualities and virtues.” In other words, Roosevelt here is lauding decisiveness, even when you don’t know everything…you just have to act. You can’t wallow in uncertainty.
Ellenberg disagrees, and wields a surprising authority as his rebuttal: the celebrated poet John Ashbery. In the poem “Soonest Mended,” Ashbery includes the following line that Ellenberg holds forth to encompass his own view of the world. “For this is action,” writes Ashbery, “this not being sure.” It’s all about uncertainty, once again—being comfortable with it, knowing how to handle it.
“The saying, ‘Let’s consider’; the saying, ‘What can we prove and what can’t we prove?’; ‘What have we thought about and what haven’t we thought about?’—that is a kind of action,” says Ellenberg of Ashbery’s line. “It’s the kind of action that mathematicians carry out. [And] I hope that I have given people reason to believe that that is a kind of action that has moved the world, just as much as armies and planes.”
To listen to the full Inquiring Minds interview with Jordan Ellenberg, you can stream below:
This episode of Inquiring Minds, a podcast hosted by neuroscientist and musician Indre Viskontas and best-selling author Chris Mooney, also features a short interview with Tasneem Raja, author of the must-read new article “We Can Code It: Why computer literacy is key to winning the 21st century” in Mother Jones, and a discussion of new findings about autism and possibly how to stop it—by making brain cells better able to communicate with one another.
To catch future shows right when they are released, subscribe to Inquiring Minds via iTunes or RSS. We are also available on Stitcher and on Swell. You can follow the show on Twitter at @inquiringshow and like us on Facebook. Inquiring Minds was also recently singled out as one of the “Best of 2013” on iTunes—you can learn more here.















