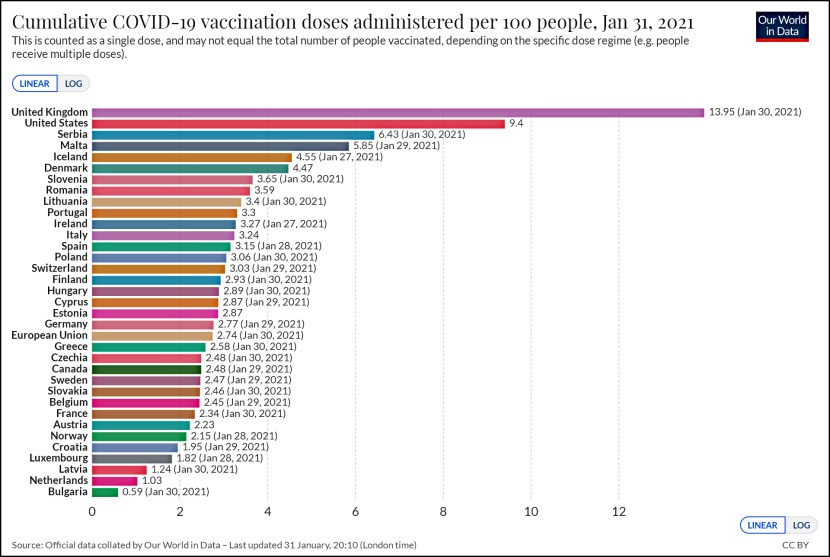
Craig Callender is tired of people misusing Heisenberg’s uncertainty principle by claiming that it’s really all about measurement. The most common example of this trope is that since measuring a particle’s velocity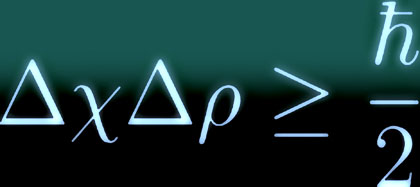 
changes the particle’s velocity, its velocity is inherently uncertain.
But it’s really more fundamental than that. Quantum uncertainty is a basic feature of the universe. It exists even if nothing is being measured:
Think of quantum mechanics as an oddsmaker. You consult the theory, and it provides the odds of something definite happening. You ask, “Oddsmaker, what are the chances of finding this particle’s location in this interval?” and the equations of the theory answer, “25 percent.” Or “Oddsmaker, what are the chances of finding the particle’s energy in this range?” and they answer, “50 percent.”
The quantum oddsmaker can answer these questions for every conceivable property of the system….The uncertainty principle simply says that for some pairs of questions to the oddsmaker, the answers may be interrelated. Famously, the answer to the question of a particle’s position is constrained by the answer to the question of its velocity, and vice versa.
Fine. But we need an EZ-to-understand way to explain this. Can we come up with a real-world example in which setting the odds of one event affects the odds of a second, seemingly independent event?
In a strict sense, we can’t. That’s the whole point of being independent: the two events don’t affect each other. But this shortcoming is shared by every analogy that attempts to explain quantum mechanics. The macro world just flatly doesn’t work like the quantum world, so the best we can hope for is something that’s kind of close. It won’t be technically correct—nothing will be—but it will get the idea across.
Just to get you started on this, here’s an example of two events: the odds of Mitt Romney being elected president and the odds of Paul Ryan being selected as Romney’s running mate. (Pretend it’s June of last year.) Romney’s odds of winning will probably affect whether he feels like he needs to take a chance on a running mate like Ryan. At the same time, the odds of choosing Ryan affect Romney’s chances of winning. Changing the odds of either event inherently affects the odds of the other.
Now, these are obviously not independent events, so it’s a lousy example. We need something that has at least the illusion of independence. But remember: we’re not looking for something where one event affects another event. That’s easy. We’re looking for something in which setting the odds of one event affects the odds of a second event, and vice versa. Any ideas?
